Arithmetic Circuits

TODO

Key Concepts

Adder circuits combine bits	A complex adder circuit performs 2's complement addition on 2 sets of bit strings. In the Full Adder configuration, this circuit manages the carry function
Subtractor circuits reduce bits	A complex subtractor circuit performs 2's complement subtraction on 2 sets of bit strings. In the Full Subtractor configuration, this circuit manages the borrow function

Terms

Term	Meaning
Arithmetic Function/Circuit	Operation that processed input signals into a mathematical output. i.e. ADD, SUBTRACT.
Circuit	Group of transistors that implement logic, control, or storage capability in hardware. AKA Gate.
Input/Output	Electrical or binary signals sent into or received out of a transistor, circuit, or arithmetic function.
Invert/Inversion	Switching a value/state to its opposite reference value/state. i.e. binary 1 is inverted into a binary 0.
Logic Function/Circuit	Operation that processed input signals into a boolean output. i.e. AND, OR, NOT.
N-Type Transistor	Transistor that outputs the same reference/boolean value as its input.
P-Type Transistor	Transistor that outputs the opposite reference/boolean value than its input.
Ripple circuit	A set of identical circuits chained together to cause an output from one circuit feeds the next circuit, and affects the next circuit's result. Common in arithmetic circuits that require carry/borrow interactions between values.
Storage Function/Circuit	Operation that retains input signal (single bit) between clock cycle. i.e. STORE, RETRIEVE.
Transistors	Electronic devices used to represent binary 1 or 0 in hardware.
Truth Table	A tablature representation of all if a circuit's inputs and outputs.

Introduction

Performing mathematical operations is a fundamental capability for computers. In this section we review Addition and Subtraction circuits. There are other circuits to performs other basic and complex math operations.

Download the Logisim Examples collection to examine in Logisim Circuit Simulation Tool

Adder

This circuit performs addition of 2 1-bit values

Half Adder

A simplifies adder circuit handles adding 1 binary bits, producing a Sum and Carry_out

The Half designation is because it does not handle a Carry_in. Therefore, the Half Adder is an good circuit to learn first, but is not used in practice

A	B	Sum	Cout
0	0	0	0
0	1	1	0
1	0	1	0
1	1	0	1

Following the algorithm to create a circuit diagram from a truth table, the following circuit is created

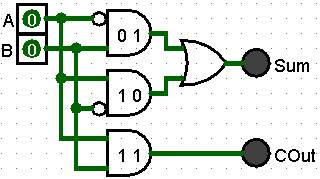
The circuit has two (2) AND gates to handle a 0,1 and 1,0 input. Both of these inputs result in a one (1) output for Sum

A Carry_in only occurs when the two inputs are both 1.

The two (2) AND gates handling 0,1 and 1,0 inputs are functioning together like an XOR gate. Therefore, we can simplify the circuit by using a single XOR gate to handle the Sum portion of the Half Adder.

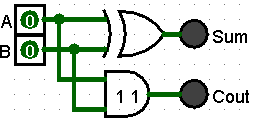
Full Adder

To be useful in most situations, a Full Adder is required. It behaves like a Half Adder and includes Carry_in, therefore it handles all possible inputs and outputs used to add 2 bits.

A	B	Cin	Sum	Cout
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

There are four (4) different possible combinations of bits added together:

1. All three (3) input bits are zero (0) - Resulting in Sum 0 and C_out 0
2. Only one (1) input bit is one (1) - Resulting in Sum 1 and C_out 0
3. Two (2) input bits are one (1) - Resulting in Sum 0 and C_out 1
4. All three (3) bits are one (1) - Resulting in Sum 1 and C_out 1

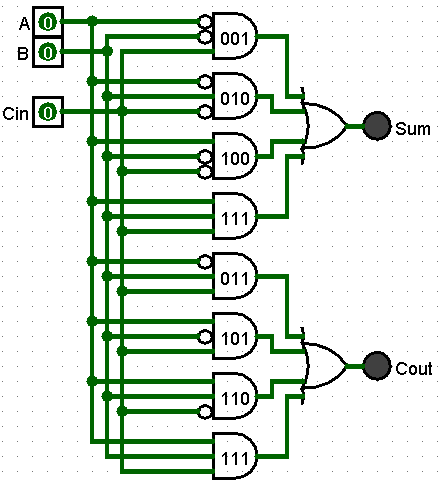
The above circuit has 2 sets of redundant AND gates (101 and 111). The circuit diagram simplifies to the following

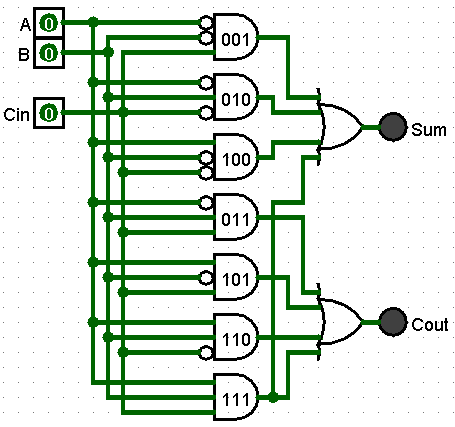
Full Adders have a simplified component symbol with the same 3 inputs and 2 outputs.

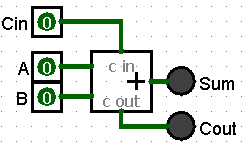
Rippler Adder

Connecting a series of Full Adders creates a circuit that will add two (2) multi-length bit strings together. The term Ripple denotes how the Carry_in and Carry_out of individual Full adders are chained together, connecting a Carry_out from a less significant bit place to the next most significate bit's Carry_in. The Carry results Ripple thought the circuit quickly (in the same clock cycle) to produce the sum of all the bits.

The Carry_out from the last Full Adder is considered Overflow for a 4-bit system. It may set a flag for the program to check. It may connect to a Carry_in of another 4-bit Ripple Adder circuit.

Note the initial Carry_in (to the least significant bits being added) is hard-coded to zero (0). This first Adder is functionally a Half adder. However, circuit designers prefer all parts be the same, so in practice all Adders are Full adders.

Four (4) bits in the A bit string (designated by A₃A₂A₁A₀) are added to the Four (4) bits in the B bit string (designated by B₃B₂B₁B₀)

Each A_n and B_n bit are input into a Full adders. The Carry_out from the previous Full Adder feeds into the Carry_in of this Full Adder. The A_n is output.

Ripple Adders can be shown on a circuit diagram with multi-bit inputs and outputs

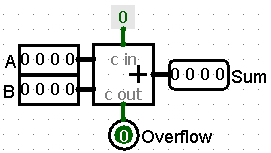
Subtractor

Half Subtractor

Like the Half Adder, the Half Subtractor does not handle the third inputs value, Borrow_in.

A	B	D	Bout
0	0	0	0
0	1	1	1
1	0	1	0
1	1	0	0

Following the algorithm to create a circuit diagram from a truth table, the following circuit is created

Reading a line from the truth table is A - B = D, B_out was borrowed from the higher significant value.

Line 2: 0 - 1 = 1 after borrowing 1

  1 0        0 10 (borrowed 1 from 2's column)
- 0 1  ->  - 0 1
  ---        ---
             0 1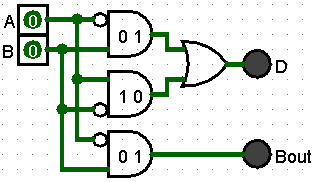

The circuit has two (2) AND gates to handle 0,1 and 1,0. Both of these inputs result in a one (1) for the Difference output.

A third AND gate handles 0, 1 input that outputs a one (1) for Borrow_out.

The circuit contains to two (2) AND gates for inputs 0, 1. IT can be simplified by removing the redundant AND gate and connecting the output to Borrow_out

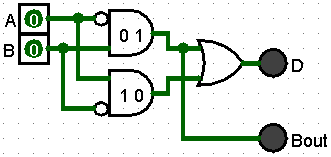
Like the Hald Adder, the two (2) AND gates handling 0,1 and 1,0 inputs are functioning together like an XOR gate. Therefore, we can simplify the circuit by using a single XOR gate to handle the Sum portion of the Half Adder.

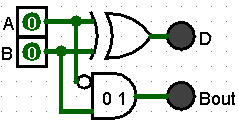
Full Subtractor

The missing input, B_in, is added to the truth table to make if a Full Subtractor. This input is 1 if the previous column (1 step less significant) had to borrow from this column

A	B	Bin	D	Bout
0	0	0	0	0
0	0	1	1	1
0	1	0	1	1
0	1	1	0	1
1	0	0	1	0
1	0	1	0	0
1	1	0	0	0
1	1	1	1	1

This is a Full Subtractor created using the algorithm and it has been simplified.

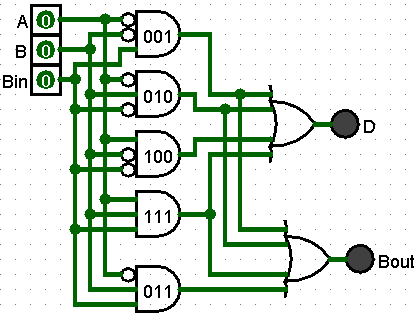
Three (3) of the AND gates from the D circuit are the same for the B_out, 001, 010, and 111.

Full Subtractors have a simplified component symbol with the same 3 inputs and 2 outputs.

Rippler Subtractor

Like the Adder, Subtractors can be connected in series for create a multi-bit subtraction circuit. The 4-bit inputs and outputs work the same as the Adder

The Borrow_out from the last Full Subtractor is considered Underflow for a 4-bit system. It may set a flag for the program to check. It may connect to a Borrow_in of another 4-bit Ripple Subtractor circuit.

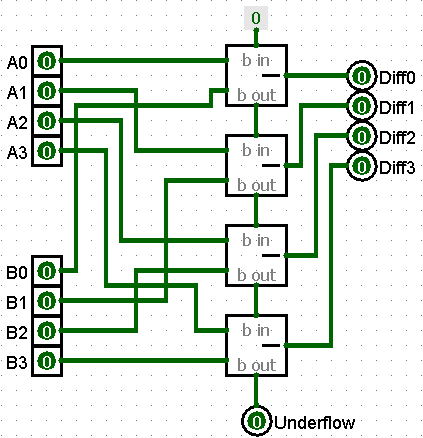
Ripple Subtractor can be shown on a circuit diagram with multi-bit inputs and outputs

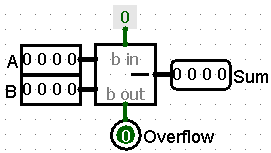
Conclusion

Single-bit addition and subtraction circuits are combined into multi-bit circuits that cas operate on multiple bit strings. And, these complex circuits can carry an borrow when needed.

The Ripple effect of information flowing though these complex circuits quickly settle out to produce a final answer.