Decimal Values

Review base 10 number system and recall how you learned to perform arithmetic operations

Key Concepts

Base 10 Number System	The number system you learned in early elementary school
Why do humans use base 10 as a default?	Likely because we started counting with our fingers. As numbers got more complicated, we stayed with base 10
Why not use base 10 in computers?	Base 10 processes are too complicated to re-create in hardware and low-level software

Terms

Term	Meaning
Binary	Base 2 numbers.
Decimal	Base 10 numbers.
Hex or Hexadecimal	Base 16 numbers.
Place or Place Value	Value of a single number in multi-symbol value. Example: In the number 12345, the Place Value if the 3 is 300.
Signed	Numbers that represent negative, zero, and positive values.
Symbols	Written characters used to depict numbers. Symbols represent to represent Decimal are 0,1,2,3,4,5,6,7,8,9.
Unsigned	Numbers that represent only zero and positive values.

Introduction

Number System: System for expressing numbers and relationships between numbers in written form. Number System start a zero (0) and end with (Base – 1)

We are taught and use the Base 10/Decimal system almost without thinking. However, we use several other number systems at times:

• Donut shop number system (12)
  • Based on a dozen base value
  • And sometimes you get 13 donuts, a baker's dozen, but this is primarily a marketing tactic
• College schedule (3 semesters / 4 quarter)
  • If someone says "I'm taking Calc I the 2nd semester, you probably understand that to be in the spring
• College grading system (A – F)
  • You know that an A is better than a B
• Date and Time
  • 12 months in a year
  • 100 years in a century
  • 28 or 29 or 30 or 31 days in a month
  • 60 minutes in an hour
  • 12 or 24 hours in a day

We all pretty competently work in all these numbers systems. In Computer Organization we will primarily focus on three (3) systems:

• Base 10 / Decimal
• Base 2 / Binary
• Base 16 / Hexadecimal

What is Base 10?

Base 10 Number System

Property	Value
# of symbols	10
Symbol Range	0 - 9
Symbols	0 1 2 3 4 5 6 7 8 9
Place Value Factor	10

Also referred to as Decimal and Denary system, Base 10 is a system commonly used by humans to refer to integer values or quantities

Base 10 is the name for the system commonly used by modern humans to count things. The 10 is the number of symbols used to represent quantities. Each symbol (digit) represents a single quantity in the range of symbols 0 -9.

Unlike Roman Numerals, no digit has an additive ot subtractive action on an adjacent digit

The 10 in Base 10 identifies the number of single digit symbols in the system

The largest symbol is Base - 1

9 in Base 10

Positional Notation

AKA Place Value

In order to represent values larger than 9 in Base 10 without adding new symbols, there needs to be a rule it calculate the value of an adjacent digit in a group of digits (number string)

The position of each symbol are essentially a weighting (factor) of each single digit according to it's position in the number string

The rule is:

• digits to the left are a lessor value
• digits to the right are higher value
• The value increase/decrease is a multiple of 10

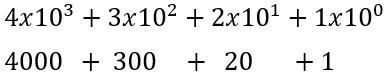
The 4 in 4321 is increased by 10 raised to the power of its position, 3, in the number string. Position numbers start at 0 are increase from left to right

To calculate a single digit place value:

Digit * 10 ^Position

After calculating the weighed value of each digit, sum all results for the final value

You may have noticed this is essential converting a base 10 value to a base 10 value...so nothing really seems to change. That is true and, in a strange sort of way, proves itself

We will, however, use this process/algorithm to convert other base number string to base 10

This may seem trivial, after all, you have likely known how to do this since elementary school. However, it is important to understand the process

Positional Notation for any Base

The positional notation works for other base number systems. The calculation for any base includes that base

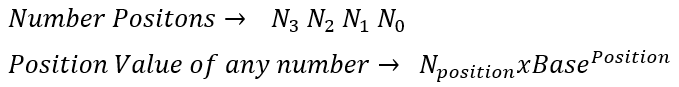
A more general formula for converting a single digit value for a given base is:

Digit * Base^{Place Value Position}

Now apply the same algorithm for calculating the value of multi-digit number string (group of digits) is:

1. Perform the single digit place value for each digit and the associated base
2. Add all the results together

Base 10 as a Human Default

It is likely that human adopted this 10 symbols to match the number of fingers on our hands...making our hands the first computation device

There is no particular importance of 10 as a number system, it is just the system most easily adopted by early humans. As humans persisted and began developing a deeper understanding of numbers, base 10 also persisted

Base 10/Decimal Number System

Origins

History

Conclusion

Decimal (base 10) number system is the de-facto standard number system used by humans. It is the system taught to children and used in business, finance, and day-to-day tasks. The metric system is based on this system.

Another Common Number System

We use other number systems for some tasks. One interesting (and complex) number system is used for Data and Time. Time is a mix of systems:

Other Number Systems

1 millennia = 1000 years

1 year = 12 months

1 month = 28 or 29 or 30 or 31 days

1 day = 24 hours

1 hour = 60 minutes

1 minutes = 60 seconds

It is impressive that most of us can follow this system with base 1000, 12, 24, and 60

Thinking in Binary

In the next section we will use our understanding of Decimal/Base 10 numbers to consider the computer's primary number system...Binary. By understanding the math behind Decimal Positional Notation, making the switch to Binary is fairly...it is the same formula with one (1) tweak