Basic Logic Circuits

Creating Simple Logic Circuits using Transistors

Key Concepts

Transistors are used to construct simple logic gate	Connecting 2, 4, or 6 Transistors in series and parallel creates a Basic Logic Circuits that behave like well-known logic functions
Basic circuits implement well-known logic operations	AND, OR, and NOT logical operations are implements using transistors to create digital computers
Basic building blocks of digital computers	Using a few different basic circuits, computer logic, storage, and control structures are created

Terms

Term	Meaning
Arithmetic Function/Circuit	Operation that processed input signals into a mathematical output. i.e. ADD, SUBTRACT.
Circuit	Group of transistors that implement logic, control, or storage capability in hardware. AKA Gate.
Input/Output	Electrical or binary signals sent into or received out of a transistor, circuit, or arithmetic function.
Invert/Inversion	Switching a value/state to its opposite reference value/state. i.e. binary 1 is inverted into a binary 0.
Logic Function/Circuit	Operation that processed input signals into a boolean output. i.e. AND, OR, NOT.
N-Type Transistor	Transistor that outputs the same reference/boolean value as its input.
P-Type Transistor	Transistor that outputs the opposite reference/boolean value than its input.
Ripple circuit	A set of identical circuits chained together to cause an output from one circuit feeds the next circuit, and affects the next circuit's result. Common in arithmetic circuits that require carry/borrow interactions between values.
Storage Function/Circuit	Operation that retains input signal (single bit) between clock cycle. i.e. STORE, RETRIEVE.
Transistors	Electronic devices used to represent binary 1 or 0 in hardware.
Truth Table	A tablature representation of all if a circuit's inputs and outputs.

Introduction

Introduction to Logic Gates - Kevin Drumm - UK YouTube Provider

This is a beginner's introduction to logic gates. It starts with an historical mention of the development of two state devices including valves and transistors, and how these led to the silicon chip. It then goes on to describe the nature and behaviour of the three main logic gates NOT, AND and OR in terms of electrical voltages, binary digits (bits) and truth tables.

Copyright TODO

Simple Logic Circuits

Basic logic operations

NOT

a	b
0	1
1	0

Applying NOT to something typically means considering the opposite of the original things.

If the crowds are NOT too big, we will go to the park.

In this example we are considering (or hoping) for the opposite of a big crowd.

When applied to binary values, the opposite means switching the bits to their opposite values. We will refer to this as flipping the bits. We also refer to this as Negation as it negates or reverses the bits.

NOT is the only operation we will discuss that takes 1 input. It operates on a single bit and flips.

NOR

NOR Truth Table

a	b	a OR b	NOT(a OR b)
0	0	0	1
0	1	1	0
1	0	1	0
1	1	1	0

NOR is referred to as NOT OR. It negates the results of the OR output. In effect it only output a 1 if both inputs are 0

NOR is effectively feeding the output of an OR operation into a NOT operation. It is interesting that the result is 0 unless both inputs are 0

NOR Transistors

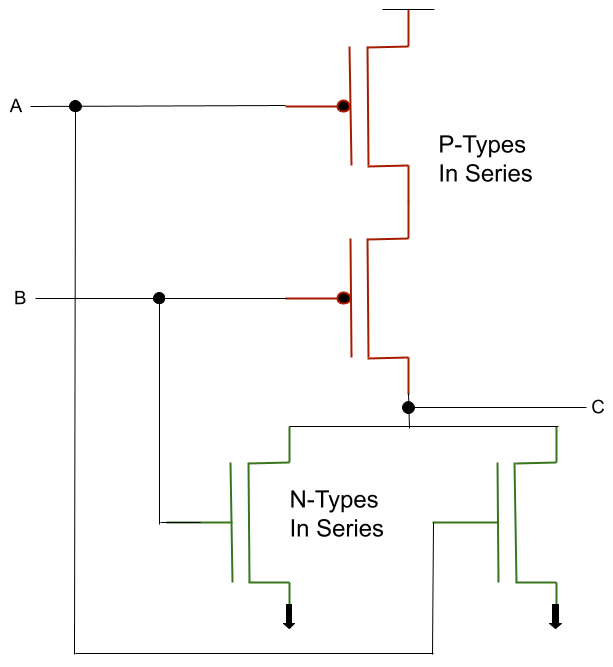
NOR Gate

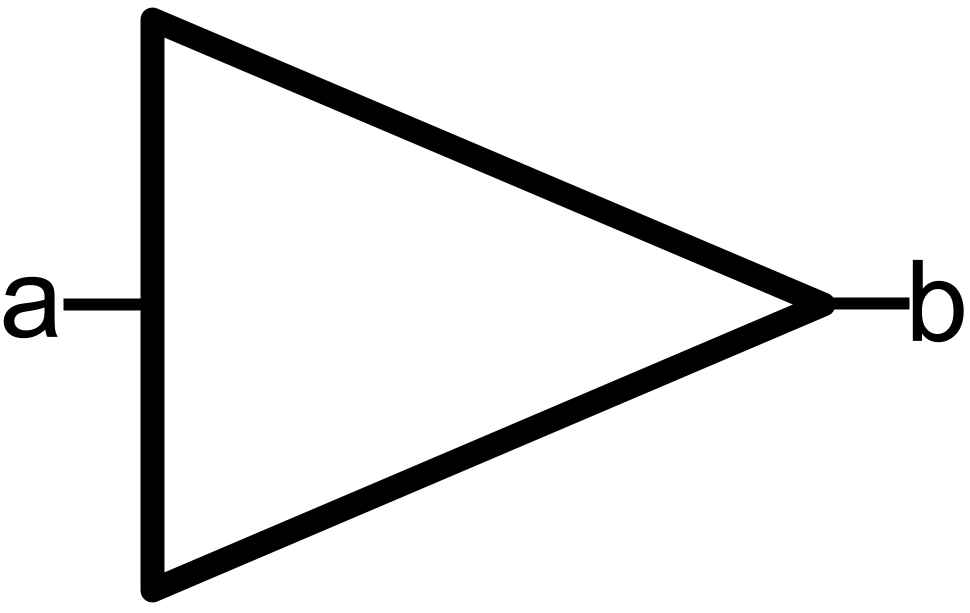
We simplify the transistor diagram into a simple circuit symbol.

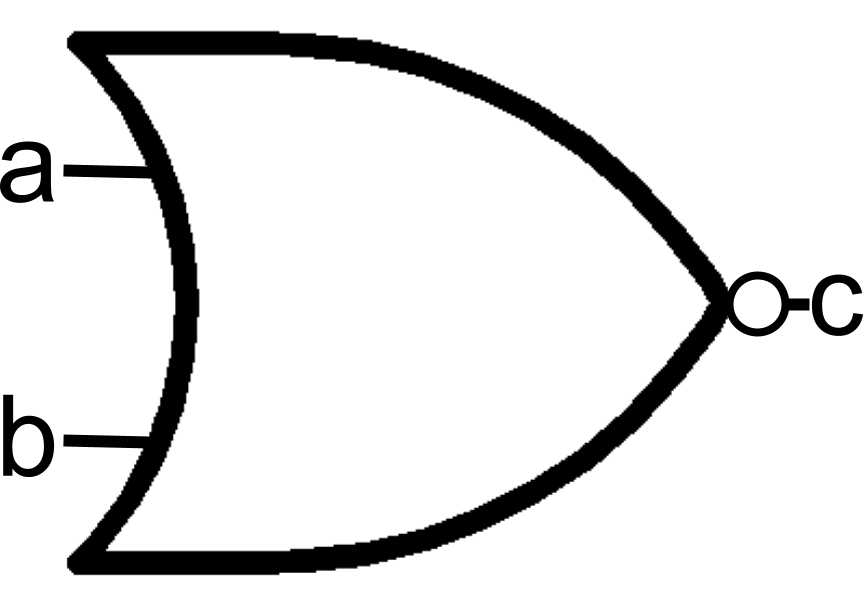
OR

OR Truth Table

a	b	c
0	0	0
0	1	1
1	0	1
1	1	1

OR Transistors

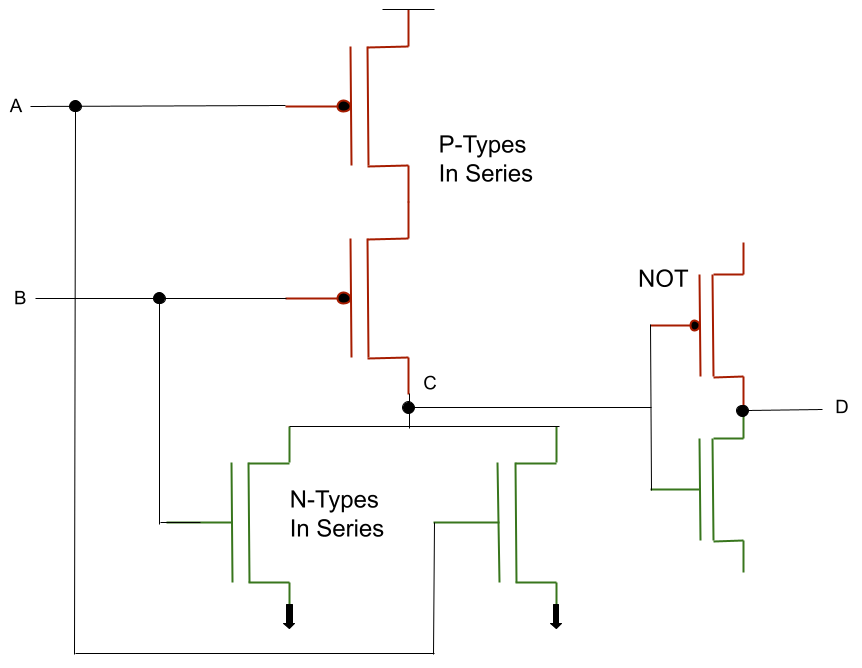
OR Gate

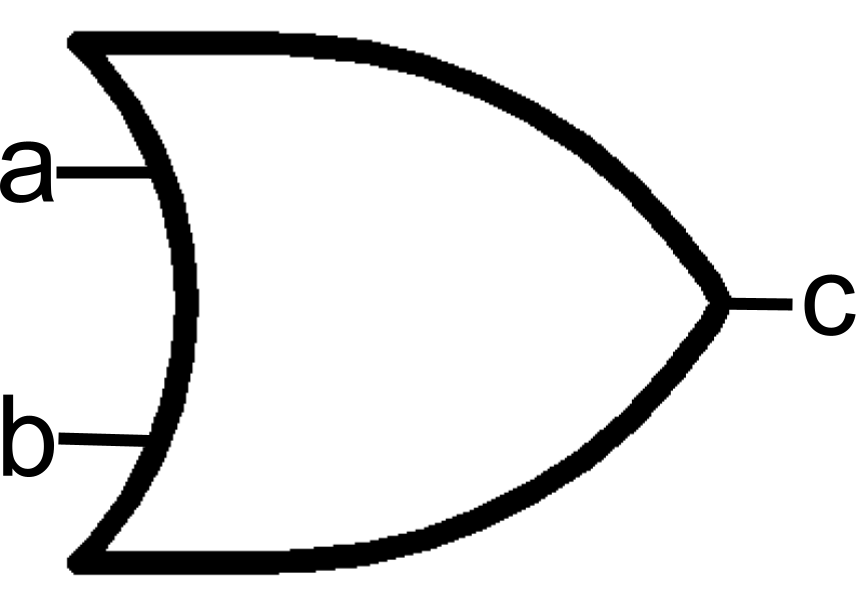
We simplify the transistor diagram into a simple circuit symbol.

Applying OR to something typically means considering any one situation enough to lead to the outcome.

We will go to the park if traffic is not too bad OR I we can get an Uber

In this example 1 or two things must be true: either traffic is low or there is an alternative way to get to the destination without driving in heavy traffic. It is also true it both things are true

When applied to binary values, OR compare two bits. If either bit is 1 the result to 1. Also, both bits can be 1 to product a 1 result. The only case that ORing 2 bits results in 0 is when both bits are 0. In the above real-life if traffic was heavy and there were no Uber rides available, the park trip is cancelled

NAND

NAND is referred to as NOT AND. It negates the results of the AND output. In effect it only output a 0 if both inputs are 1

It is not a common logic operation applied to everyday situation, but it has utility in the logic and computer circuits

NAND Truth Table

a	b	c
0	0	1
0	1	1
1	0	1
1	1	0

It is interesting that the result is 1 unless both inputs are 1

NAND Transistors

The NAND circuit requires 2 P-Type transistors in parallel and 2 N-Type transistors in series. a and b inputs are connected to one of the P- and N-Type transistor control inputs. In this configuration, the junction between the P- and N-Type pairs outputs the NAND logic.

NAND Gate

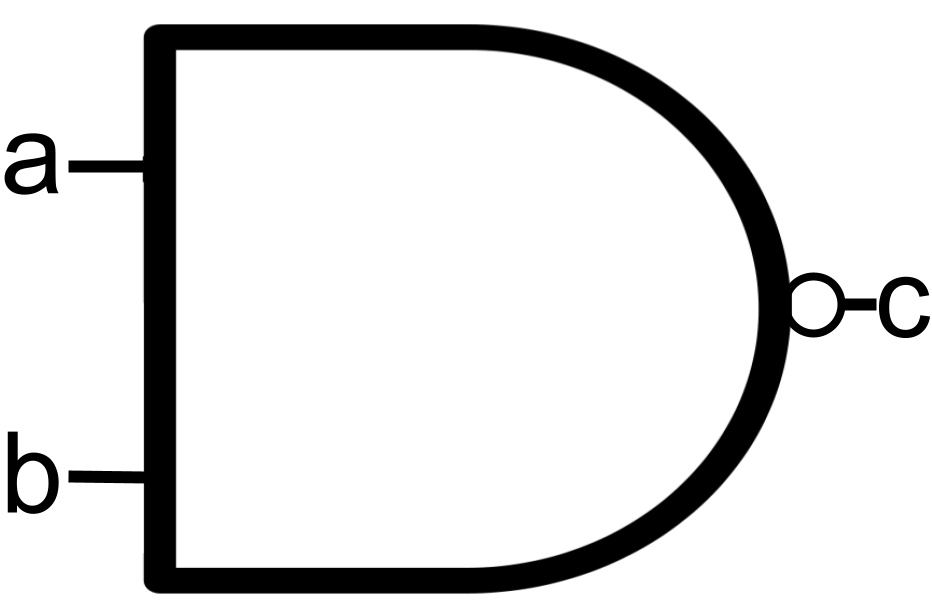
We simplify the transistor diagram into a simple circuit symbol.

AND

Applying AND to something typically means considering all situations must occur to lead to the outcome.

We will go to the park if traffic is not too bad AND I we can get an Uber

In this example both things must be true: traffic is low as well as there is an alternative way to get to the destination without driving in heavy traffic. If either one of the things is not true then no park trip. If both things are not true, the trip is also off

AND Truth Table

a	b	c
0	0	0
0	1	0
1	0	0
1	1	1

AND Transistors

AND Gate

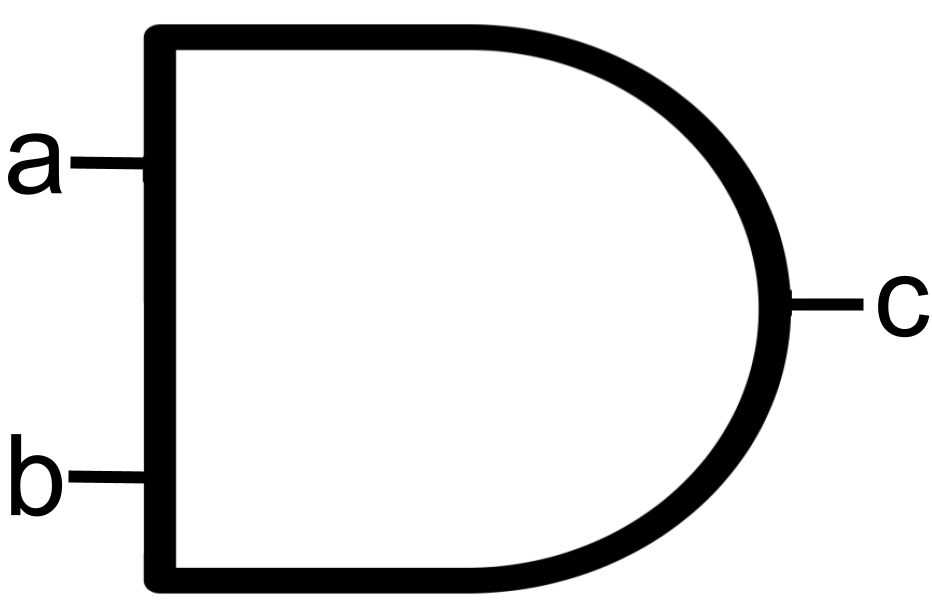We simplify the transistor diagram into a simple circuit symbol

When applied to binary values, AND compare two bits. If either bit is 0 the result to 0. If 1 bit is 0 and the other is 1 to product is also 0 result. The only case that ANDing 2 bits results in 1 is when both bits are 1. In the above real-life if traffic was heavy or there were no Uber rides available, the park trip is cancelled

XOR

a	b	c
0	0	0
0	1	1
1	0	1
1	1	0

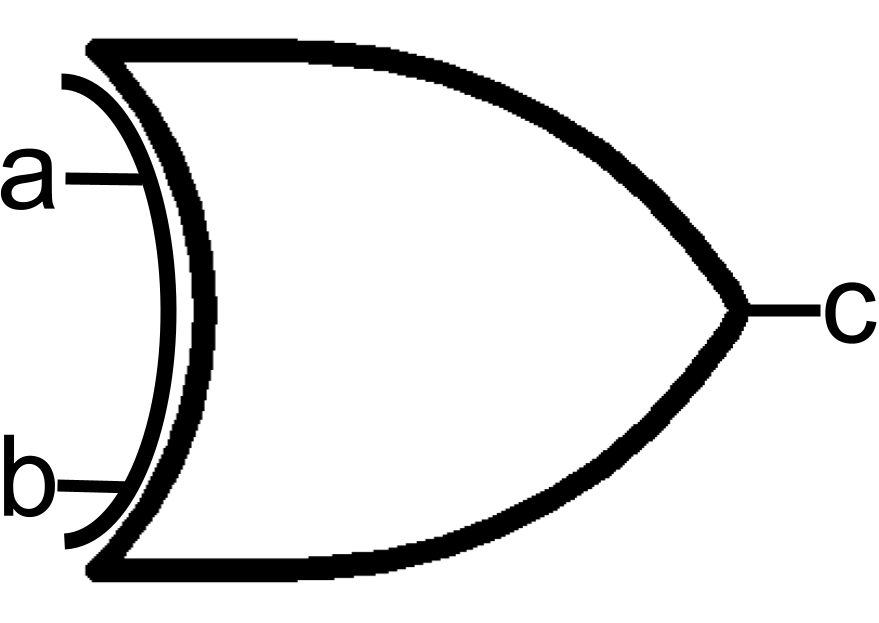
XOR is referred to as Exclusive OR. The difference between XOR and OR is the case where both bits as 1 results in 0. Another way to think of this is the two bits being compared must be different to result in 1

Logic Circuit Constructs

There are a couple of interesting things simple logic circuits can do to be made more versatile or to change their behavior.

Adding Inputs to a Logic Circuit

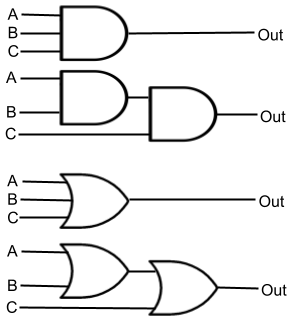
At this point all of our logic circuits have 2 inputs (with the exception of NOT). It is possible to have a logic circuit with more than two (2) inputs.

While the diagram for a 3 or 4 input AND circuit seems simple, under-the-hood it is a set of 2-input AND circuits with the output of 1 feeding an input of the next. The logical behavior still works as expected.

DeMorgan's Laws

Augustus De Morgan proposed a pair of comparisons in the field of boolean algebra that have an interesting application to computer organization. When applying negation (NOT) transformations to solution sets of AND and OR functions, he realized that negating inputs and output of one set resulted in the other.

Inverting the inputs to an OR gate, then inverting the output produces the same truth table as an AND gate.

a	b	NOT a	NOT b	NOT a AND NOT b	NOT(NOT a AND NOT b)	a OR b
0	0	1	1	1	0	0
0	1	1	0	0	1	1
1	0	0	1	0	1	1
1	1	0	0	0	1	1

Inverting the inputs to an AND gate, then inverting the output produces the same truth table as an OR gate.

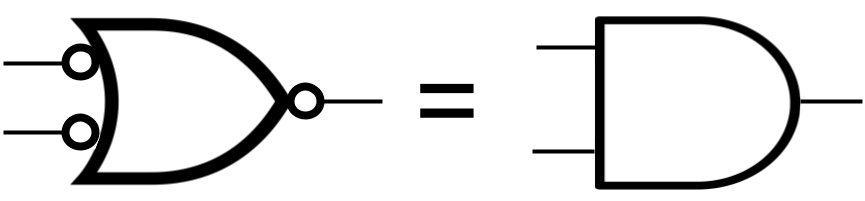
So, with only NOT and OR gates, you can produce a circuit that outputs AND results. Using NOT and AND gates will, similarly produce OR outputs.

Conclusion

Simple logic circuits are constructed of transistors. They behave like the boolean logic operations. AND, OR, and NOT are the core logic circuits. Variations of these circuits include NAND, NOR, and XOR

Two (2) input circuits can be constructed to allow additional inputs into the logic calculation. By manipulating input and output signals, one logic circuit can be made to change it's behavior.