Hexadecimal Values

Understand how base 16 (hex) number system is a shorthand to base 2 (binary)

Key Concepts

Base 16 is a compact means to representing binary values	With a little understanding, hardware and software practitioners can translate between Hex and Binary
Hexadecimal and Binary have a helpful association	16 is a power of 2...2^4. This property means each 4 binary digits concert to 1 Hex symbol, making conversions a bit simpler

Terms

Term	Meaning
Binary	Base 2 numbers.
Decimal	Base 10 numbers.
Hex or Hexadecimal	Base 16 numbers.
Place or Place Value	Value of a single number in multi-symbol value. Example: In the number 12345, the Place Value if the 3 is 300.
Signed	Numbers that represent negative, zero, and positive values.
Symbols	Written characters used to depict numbers. Symbols represent to represent Decimal are 0,1,2,3,4,5,6,7,8,9.
Unsigned	Numbers that represent only zero and positive values.

Introduction

What is Base 16?

Base 16 Number System

Property	Value
# of symbols	16
Symbol Range	0 - F
Symbols	0 1 2 3 4 5 6 7 8 9 A B C D E F
Place Value Factor	16

Base 16 (Hexadecimal or Hex) is a number system you will likely encounter in various places in Computer Science. While a bit odd looking at the start, Hex is a shortcut to describing binary values in a compact manner

Converting to Base 10

The algorithm used to convert from Binary to base 10 works here, just changing the base to 16. We also need to use the lookup table (above) to convert each Hex value to Decimal

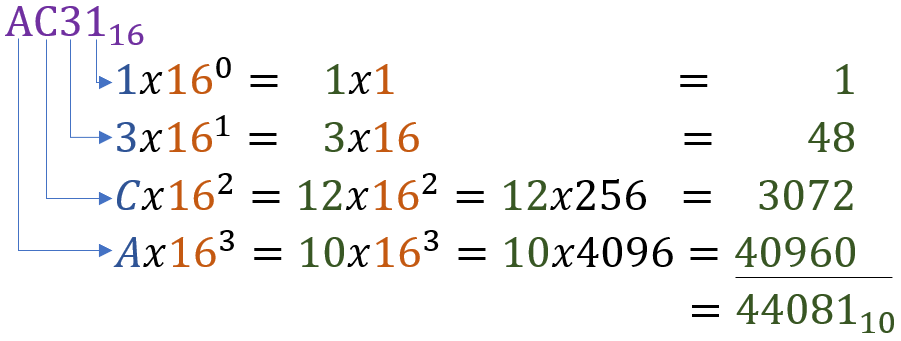
Algorithm

Recall that number positions in a number string start at zero. So the value in the 1st position is said to be in position 0

Also, we will be raising 16 to the power of the position, because the original number is in Base 16

1. Convert each Hex value to Base 10 using the lookup table
2. Multiply the resulting Base 10 value by 16 raised to the power of the value's position
3. Add the result to the final Decimal result
4. Repeat for all Hex values

You'll Need a Calculator for this

Raising 16 to increasing powers is not easy to do in your head. And, in the above example, notice each Hex place value grows substantially. This is why Base 16 results in very compact numbers that represent large Decimal values

16^2

Converting to/from Binary

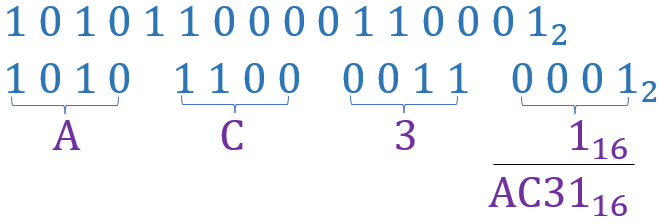
This is where Hex is that compact representation of binary

Each Hex value represent 1 4-bit Binary string. And a 4-bit Binary value can be represented by a single Hex value

Binary	Decimal	Hex		Binary	Decimal	Hex
0000	0	0		1000	8	8
0001	1	1		1001	9	9
0010	2	2		1010	10	A
0011	3	3		1011	11	B
0100	4	4		1100	12	C
0101	5	5		1101	13	D
0110	6	6		1110	14	E
0111	7	7		1111	15	F

Conclusion

Converting from Hexadecimal to Decimal is the same algorithm and Binary to Decimal, just using a different base number in the conversions.

Hexadecimal is useful in expressing binary values in a compact format. Each Hex symbol represents exactly four (4) binary numbers.