Representing Numbers in Binary

Using bits to represent useful numeric type

Key Concepts

We can use Binary to represent whole and fractional numbers Organizing bits into standard formats, we can represent integers, fix- and floating-point fractional numbers. Each architecture defines how it maintains these values/ Representing negative and positive numbers requires some additional processing Number systems do not contain a symbol for negative values. When using numbers in any system we agree upon a format to indicate negative numbers. In computer architectures the use of a 'sign bit' is the agreed upon process to including negative and positive states of a number.

Terms

Term	Meaning
Binary	Base 2 numbers.
Decimal	Base 10 numbers.
Hex or Hexadecimal	Base 16 numbers.
Place or Place Value	Value of a single number in multi-symbol value. Example: In the number 12345, the Place Value if the 3 is 300.
Signed	Numbers that represent negative, zero, and positive values.
Symbols	Written characters used to depict numbers. Symbols represent to represent Decimal are 0,1,2,3,4,5,6,7,8,9.
Unsigned	Numbers that represent only zero and positive values.

Introduction

The following table is a quick reference between binary and decimal numbers 0 - 15. For unsigned decimal numbers, 4 bits is all that in needed to represent 0 - 15

Binary2	Decimal10		Binary2	Decimal10
0000	0		1000	8
0001	1		1001	9
0010	2		1010	10
0011	3		1011	11
0100	4		1100	12
0101	5		1101	13
0110	6		1110	14
0111	7		1111	15

Unsigned Integers

Using the conversion algorithm we learned in Binary Values, you can verify the above table. Each binary value converts to the corresponding decimal l value.

Binary to Decimal Algorithm

Recall that array indexes start at zero(0). Number positions in a number string also start at zero. So the value in the 1st position is said to be in position 0

1. Multiply a Binary value by 2 raised to the power if the value's position
2. Add the result to the final Decimal result
3. Repeat for all Binary values

The number of decimal values that can be represented in a fix number of binary digits (bits) is 2^{num of bits}. The minimum value is 0 and the maximum is is 2^{num of bits}.

4 bits can represent 2⁴ or 16 values. 0 to 15₁₀

16 bits can represent 2¹⁶ or 65536 values. 0 to 65535₁₀

Signed Integers

To be truly useful, we need to be able to represent negative (signed) values in binary. In order to accomplish this, we will sacrifice 1 bit to stand in for the +/- sign.

Before proceeding, we need to understand how to add 1 binary values. We will explore this moreIt is just like adding 2 decimal numbers:

A Full Adder

A	B	Cin	Sum	Cout
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

There are four (4) different possible combinations of bits added together:

1. All three (3) input bits are zero (0) - Resulting in Sum 0 and C_out 0
2. Only one (1) input bit is one (1) - Resulting in Sum 1 and C_out 0
3. Two (2) input bits are one (1) - Resulting in Sum 0 and C_out 1
4. All three (3) bits are one (1) - Resulting in Sum 1 and C_out 1

The Sign Bit

Computer designers chose the most significate bit to represent the sign of the remaining bits. 0 in the left most Sign Bit position indicates a positive value for the entire bit string. A Sign Bit of 1 indicates a negative value.

We can still represent 2^{num of bits} values with a Sign Bit, however the maximum value represented is now 2^{num of bits - 1}

4 bits can represent 2⁴ or 16 values. -8 : +8₁₀

16 bits can represent 2¹⁶ or 65535 values. -32786 : 32786₁₀

Binary2	Decimal10		Binary2	Decimal10
1111	-7		0111	+7
1110	-6		0110	+6
1101	-5		0101	+5
1100	-4		0100	+4
1011	-3		0011	+3
1010	-2		0010	+2
1001	-1		0001	+1
1000	-0		0000	+0

We can see in this updates table that 111₂ is still 7₁₀, however with the sign bit is 1 (1111), the value is -7₁₀. Check a couple of other values...for any two values where the three (3) least significate bits are the same, it is the same value, but positive is the sign bit is 0 and negative if it is 1.

Do you see any problems with this new table?

• Mainly there are two (2) bit strings that represent zero (0)
• And one if this is a negative zero (-1)

2's Complement

To fix these issues, signed binary values use a conversion algorithm called 2's Complement

Video on 1's and 2's complement representations of values

Table of 2's Complement Value in 4 bits

Binary2	Decimal10		Binary2	Decimal10
			0000	0
1111	-1		0001	+1
1110	-2		0010	+2
1101	-3		0011	+3
1100	-4		0100	+4
1011	-5		0101	+5
1010	-6		0110	+6
1001	-7		0111	+7
1000	-8

Converting 2's Complement Binary to Base 10

In a 2's complement system, the conversion is the same as unsigned, however the sign bit is negative

This example uses 8 bit values where the least 7 bits are the value/magnitude of the base 10 number being represented and the most significant bit is the sign bit

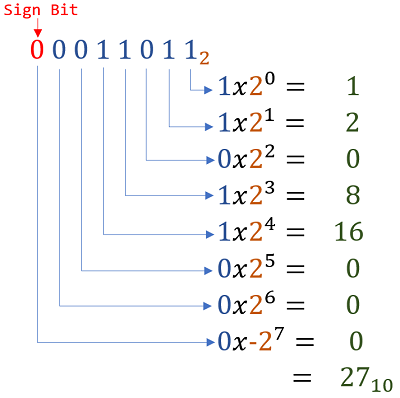
Convert a 2's Complement value to it's opposite value

In Base 10 we can multiply a value by -1 to switch from negative to positive -or- positiver to negative. In 2's complement binary were can perform the same conversion, using a 2-step process

Algorithm to convert between positive and negative values in 2's complement

1. Flip all the bits
2. Add 1 to the resulting bits

Step	bit value	decimal value
Starting Value	0101	5
Flip the Bits	1010	n/a
Add 1	1011	-5

note: the decimal value after flipping the bits does not matter

Use the above algorithm to test yourself

What is the 2's complement value for +25₁₀ (011001₂)

Step	bit value	decimal value
Starting Value	011001	25
Flip the Bits	100110	n/a
Add 1	100111	-25

Sign Extension

It is probably second nature that 25₁₀ and 00000025₁₀ are the same value. The most significant zeros do not change the value of the number. They are unnecessary.

-25₁₀ and -00000025₁₀ are also the same and unnecessary.

2's complement binary values have a similar property, but a little different that decimal values.

6₁₀ = 0110₂ = 00000110₂

We can lengthen a positive binary value by adding zeros (0) to the most significant bits without changing the value.

-6₁₀ = 1010₂ = 111111010₂

We can lengthen a negative binary value by adding one (1) to the most significant bits without changing the value.

In effect, the additional ones or zeros are extending the sign bit. When removing the extra bits, the original sign bit must be retained so that the value keeps its original sign

In computer architecture, sign extension is not unnecessary. As we will see in logic circuits, sometimes binary value of 16 or 32, or 64 bits long is required, even if the original bit string was shorter. A hardware circuit can copy the sign bit as many time as needed to create the desired length bit string before executing certain instructions.

Fixed-Point

In order to represent fractional values in binary, a fixed number of the least significate bits can be designated as the fractional part. The remaining most significant bits are the whole number part

An architecture will define how many bits are used for the fractional and whole-number part. There is no bit used to hold the decimal point in memory. The hardware is configured to always, in the case of this example, use the 3 least significant bits.

The conversion from fixed point binary to base 10 fractional is the same as a whole number, however the fractions bits are multiplied by a fractional power of 2.

In base 10 we refer to the fractional digits as 10^ths,100^ths, 1000^ths

In binary, maybe we call these fraction bits 1-2^th,2-2^ths, 3-2^ths. Maybe not, since these parts do not have true names.

Regardless of the names, It falls to the assembly programmer to identify bits strings that represent fixed-point values. Then the architecture can apply the correct conversion to generate the correct decimal value.

Conclusion

Based on the architecture's design, integer and fractional values can be represented in binary. Because digital circuits do not have a decimal-place indication, the assembly program must use the architecture's rules on using fractional values.

Binary and digital circuits no have have a way to represent a negative value...only positive numbers. Using one of the value's bits to indicate the sign and the 2's Complement algorithm, binary values can be stored, used, and modified.